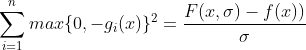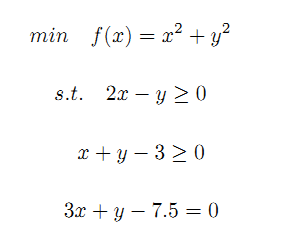惩罚函数
惩罚函数也叫乘子法,求解带约束的非线性规划问题时,常用KKT条件列出满足条件的方程组,解方程组后即可得到最值点,当满足KKT条件的方程组是一个非线性方程组,利用计算机求解很难给出通用算法。本篇介绍的惩罚函数可以将一个带约束非线性问题转化为无约束的非线性规划,而无约束线性规划可以用梯度法等实现求解,利用惩罚函数更方便我们制成计算机算法,在现代计算机算法中,凡涉及到求解最值,都会大量的运用惩罚函数或者借鉴惩罚函数思想。
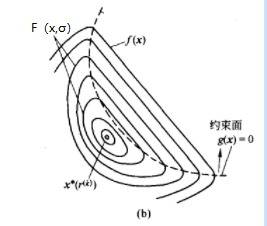
惩罚函数可以分为外点法和内点法,其中外点法更通用,可解决约束为等式和不等式混合的情形,外点法对初始点也没有要求,可以任意取定义域内任意一点,外点法是真正的将问题转化为无约束问题;而内点法初始点必须为可行区内一点,在约束比较复杂时,这个选择内点法的初始点是有难度的,并且内点法只能解决约束为不等式情形。
一、 外点法
首先引入一个带等式约束的非线性规划问题:
min f(x)
s.t. hi(x)=0 i=1,2,3,...m
目标函数f(x)是非线性函数,约束条件为m个等式,上面问题中可以通过拉格朗日乘数法或KKT条件获得最值,而惩罚函数的解决方案是引入一个新的函数:
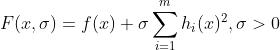
上式中F(x,σ)为惩罚函数,σ称为惩罚因子,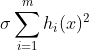
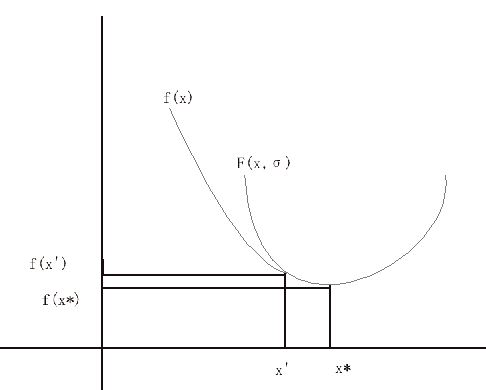
x'点是原问题最小值点,即x'也是可行点,满足原问题所有等式条件,F(x,σ)与f(x)在该点函数值相等:F(x',σ)=f(x'),x'点是目标最值点。通过观察可以发现,虽然F(x,σ)是f(x)的上界函数,但最值F(x*)是小于f(x')的,这是由于F(x*)是F(x,σ)是在无约束情形下的最小值,F(x,σ)参数x可取值范围比原带约束的问题大的多(原问题x必须满足所有等式),极点x*是函数F(x,σ)全局最小值点,外点惩罚函数通过每轮增大参数σ,逐渐让x*逼近x',通过不断迭代计算,最终的x*便是近似的目标函数极值点x',这样一来,就实现了利用求解无约束最值得到另一个有约束问题最值。
再来看约束为不等式的情形,如求以下函数f(x)的最小值:
min f(x)
s.t. gi(x)>=0 i=1,2,3,...n
约束为不等式时,惩罚函数是下面的形式:
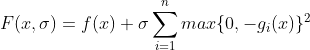
当惩罚函数参数x在可行区内时,惩罚项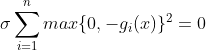
g(x)>=0为不等式约束,F(x,σ)函数极值点x*初始时在可行区外,点x*往g(x)=0方向移动时,F(x*,σ)函数值逐渐增大。在可行区内,F(x,σ)与f(x)等值线是一样的,代表两个函数在可行区内函数值相同,约束问题极值点x'一定是在可行区内,即在上图虚线上以及虚线右侧的范围内;在虚线左侧时F(x,σ)极值F(x*)小于f(x')。惩罚函数解决不等式约束时,是通过调整参数σ,让x*逐渐接近可行区, 从而得到约束极值点x'。
通过上面两种情形的分析,可以发现外点法是从可行区外慢慢接近边界,在接近的过程中计算每个阶段极值点,一旦到达可行区范围内,该极值点即为原带约束非线性规划的极值点,接下来还有最后一个问题,为什么增大参数值σ可以让极值点x*接近可行区,以公式(2)为例,做适当变换可得:
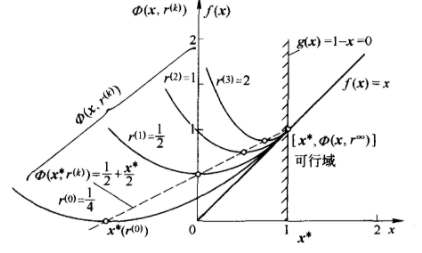
σ增大时,惩罚项将逐渐等于0,代表F(x,σ)等值线整体逐渐向可行区移动。这里也可以看出,σ之所以叫惩罚因子是对惩罚函数的极值点不在可行区时,对惩罚函数进行相应的惩罚,因此,调整惩罚因子将移动惩罚函数极值点,这个动态的过程可参考下图,惩罚函数Φ(x,rk)不断增大rk后,Φ(x,rk)的极值点x*不断接近目标函数f(x)极值点:
综合上面两种情形,当约束条件为不等式和等式混合时,有以下通用的惩罚函数形式:
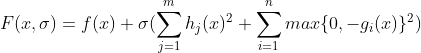
可以看到,不等式与等式约束公用一个惩罚因子σ,σ>0。根据上面的分析,接下来通过一段python代码实现外点惩罚函数,下面是一个含有两个不等式、一个等式约束的非线性规划问题:
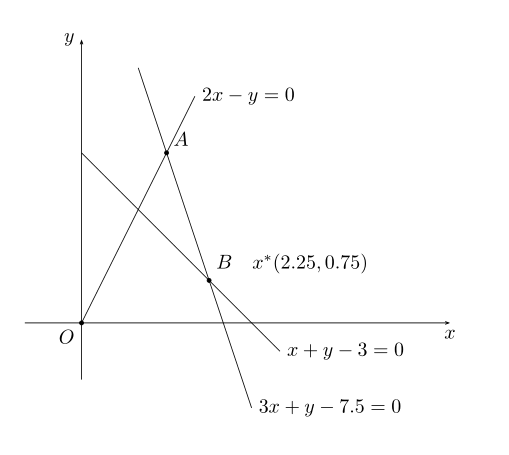
示例最优解可用以通过图形观察出来,目标函数最小值是求原点到可行区内最短距离的平方,等式3x+y-7.5=0与不等式约束所规定区域相交于A、B两点,其中在点B处(2.25,0.75)为最小值点:
import math
import sys
sys.setrecursionlimit(500)
errorRate=1e-4
stepLowerlimit=1e-5
#计算惩罚项
def punishfunc(sigma, x, y):
punishvalue=(3 * x + y-7.5) ** 2
if (2 * x - y < 0 ):
punishvalue=punishvalue+ (2 * x - y) ** 2
if ( x + y - 3 < 0):
punishvalue = punishvalue + (x + y - 3) ** 2
return punishvalue*sigma
#惩罚函数一阶导数
def P_firstderivative(stepx,x, y,gx,gy, sigma):
d1=2*(gx *stepx-x) *gx+2*(gy*stepx-y)*gy+2*sigma*(-3*gx-gy)*(3*x-3*gx*stepx+y-gy*stepx-7.5)
if (2 * x - y < 0):
d1=d1+2*sigma*(-2*gx+gy)*(2*x-2*gx*stepx-y+gy*stepx)
if(x + y - 3 < 0):
d1 = d1 + 2*sigma*(-gx-gy)*(x-gx*stepx+y-gy*stepx-3)
return d1
#惩罚函数二阶导数
def P_secondderivative( x,y,gx,gy, sigma):
d2=2*gx**2+2*gy**2+2*sigma*(-3*gx-gy)**2
if (2 * x - y < 0):
d2=d2+2*sigma*(-2*gx+gy)**2
if (x + y - 3 < 0):
d2 = d2 + 2*sigma*(-gx-gy)**2
return d2
#牛顿法实现一维搜索
def newton(x, y,gx,gy, sigma):
stepx,l,iterNum=0,1e-4,0
dx_1=P_firstderivative(stepx,x, y,gx,gy, sigma )
while abs( dx_1)>l:
dx_1 = P_firstderivative(stepx, x, y, gx, gy, sigma)
dx_2 = P_secondderivative(x,y,gx, gy, sigma)
stepx=stepx-dx_1/dx_2
iterNum = iterNum + 1
return stepx
#求每次sigma对应的最小值,sigma每次递增,逐步逼近目标函数最值
def calmin(x, y, sigma, counter):
gradpart1_x, gradpart1_y, gradpart2_x, gradpart2_y = 0, 0, 0, 0
if(2 * x - y<0 ):
gradpart1_x = 2 * (2 * x - y) * 2 * sigma
gradpart1_y = 2 * (2 * x - y) * -1 * sigma
if ( x + y - 3 < 0):
gradpart2_x = 2 * (x + y - 3) * sigma
gradpart2_y = 2 * (x + y - 3) * sigma
gradpart3_x = 2 * (3 * x + y - 7.5) * 3 * sigma
gradpart3_y = 2 * (3 * x + y - 7.5) * 1 * sigma
gradx = 2*x + gradpart1_x + gradpart2_x+gradpart3_x
grady = 2*y + gradpart1_y + gradpart2_y+gradpart3_y
distance = math.sqrt(gradx ** 2 + grady ** 2)
gradx = gradx / distance
grady = grady / distance
#牛顿法一维搜索得到步长
stepx=newton(x,y,gradx,grady,sigma)
x = x - gradx * stepx
y = y - grady * stepx
punishvalue = punishfunc(sigma, x, y)
value_end = x ** 2 + y ** 2 + punishvalue
if (stepx <= stepLowerlimit ):
return x, y, value_end, punishvalue, sigma
else:
counter=counter+1
return calmin(x, y, sigma, counter)
def outpoint(x, y, sigma, c ):
_x, _y, _v, _p=x,y,0,1
while ( _p>errorRate ):
_x, _y, _v, _p, _sigma = calmin(x, y, sigma, 0)
x=_x
y=_y
sigma = sigma * c
pass
value_end = x ** 2 + y ** 2 + punishfunc(sigma, x, y)
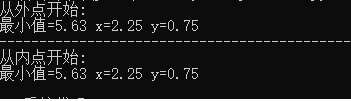
print('最小值=%0.2f x=%0.2f y=%0.2f'%(value_end,x,y))
if __name__ == '__main__':
sigma = 1#惩罚因子
c = 10
print('从外点开始:')
outpoint(0, 0, sigma, c )# 外点测试
print('-'*100)
print('从内点开始:')
outpoint(3 ,3, sigma, c )#内点测试可以看到外点惩罚函数的初始点既可在可行区外,也可在可行区内,这两种情形得到的结果是一致的,运行结果如下:
外点惩罚函数是通过outpoint()函数实现的,当惩罚项的数值小于一定值后退出循环,如惩罚项的数值未达到阈值则增大参数sigma ,再次求解惩罚函数的最小值;求解惩罚函数最小值是一个无约束最优解问题,这里使用的是梯度法,实现函数是def calmin(x, y, sigma, counter),该函数在内部确定梯度方向后,由于是求最小值,取梯度反方向,再利用一维搜索法获得最佳的步长系数,关于一维搜索可参考一维搜索这篇文章,以上代码是通过牛顿法实现以一维搜索的。
二 、内点法
内点法通常只适用约束为不等式的情形,还以之前不等式约束为例:
min f(x)
s.t. gi(x)>=0 i=1,2,3,...n
内点法如下构造惩罚函数:
与外点法相反,内点法通过不断递减参数惩罚因子σ,这是由于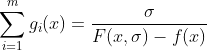
内点函数初始时必须选可行区域内一点,由于不等式约束g(x)接近0时,惩罚函数值趋近于无限大,使用梯度法求解最小值时,自然不会朝这个方向运动,内点法将不等式边界函数放置在分母中,是利用边界效应阻碍惩罚函数向函数值增大方向前进,从而起到屏障的效果。不断减小惩罚系数后,会把惩罚函数向下拉拽,当惩罚系数接近0时,惩罚函数最小值无限接近目标函数最小值。从图形上看,在边界处,惩罚函数产生一个'陡峭'跃迁:一边是无穷大,一边是最小值点。
内点法本质上仍然是一个有约束规划问题,由于向非可行区g(x)<0移动过程中会经过g(x)=0,而在g(x)=0处受到代数法则和梯度性质,阻绝了惩罚函数向非可行区移动,这就间接地将原问题变为一个无约束的问题。比起外点法,内点法具有迭代次数少的优点,在对算法时间要求较高的场合下推荐使用。内点法最大难点主要在第一步,很多情况下找到初始可行点是非常困难的,往往找到可行点已经接近最优解了;其次,内点惩罚项不管是选择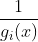
| 上一篇 KKT条件 | 下一篇 SVM支持向量机详解 |
| 评论区 | |