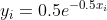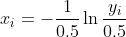有时候需要利用计算机生成指定连续分布的随机数，比如指数分布、正态分布、伽马分布等，一般我们会用相同数量的[0,1]之间均匀分布的随机数去生成其他形式连续分布随机量。本篇适用于连续的概率分布函数，并不适合于生成离散分布的随机数，首先介绍并证明并以下定理。

      一、定理:有连续随机变量x,x的累积分布函数y=F(x)也是连续函数,那么函数值y也是一个随机变量，且y是均匀分布。

     1.1 定理证明

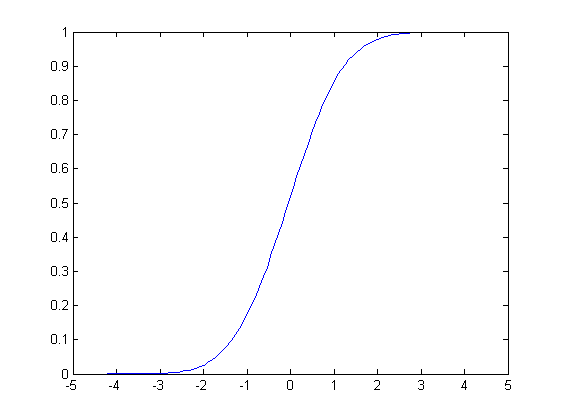
      这个定理读起来非常拗口，其实用大白话说就是y=F(x)是随机变量x的分布函数，学过概率论的都应该知道分布函数肯定是一个递增函数，分布函数一般都如下图所示：

定理要求这个分布函数还得连续，满足这个条件后，这个分布函数的值y也是一个随机变量，并且y是[0,1]之间均匀分布的随机变量，证明如下：

这个定理告诉我们，因为这个分布函数是连续、单调递增的，那么其反函数x=F^-1(y)也一定是连续、单调递增的，这就保证了[0,1]之间均匀的随机数y与目标连续分布的随机数x存在一一对应的关系。比如需要生成10个λ=0.5的指数分布随机数时，只要先生成10个[0,1]之间均匀分布的随机数y₁,y₂,y₃...y₁₀，然后利用其分布函数的反函数:

就能依次生成10个指数分布随机数： x₁,x₂,x₃...x₁₀。

    1.2 蒙特卡罗法

    定理说明了一个均匀随机分布随机变量与另一个分布随机变量的一一对应关系，是一种函数关系，所谓一一对应关系数学上称为映射，具体说是一种双射（单射且满射），以上的定理运用了一个[0,1]之间均匀分布变量y一一对应于随机变量x,这样一来就可以生成了一系列目标分布的随机变量，y在这里其实代表了一个概率（概率不就是一个0,1之间的数值吗？），一个分布函数上的具体值。需要强调，并不是说随机变量等于x时的概率是y,由分布函数定义知连续分布单点概率值都是0，连续概率是指随机变量X(大写)小于等于x的概率是y，可表达为：P(X<=x)=F(x)=y，所以定理中要求分布函数实际上是一个累积分布函数。理解以上内容后我们来介绍蒙特卡罗法的一个应用---利用蒙特卡罗法计算积分值。

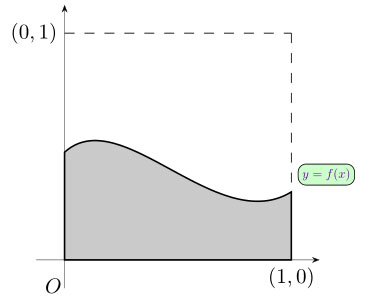
上面的函数f(x)的定义域是[0,1],值域也是[0,1],f(x)无法通过换元法和分部积分法等传统方法求积分时，可利用以上定理来实现，可以通过生成一系列随机变量并求其分布的概率，最后得出的概率就是积分值。

      在具体应用时，定义域和值域可能不在[0,1]之间，但不妨碍我们使用蒙特卡罗法，利用换元法分别构造三个概率密度函数p(x,y)、p_X(x)、p_Y(y)后，就可以像本例一样使用蒙特卡罗法。蒙特卡罗法也是定理一的具体应用：先生成多个二维随机变量(xi,yi）,然后利用二维均匀分布求出概率（y_i≤f(x_i)的概率），这个概率值即为目标函数积分值；而之前生成随机数的例子中则是生成一系列均匀分布概率值，然后利用这些概率值结合反函数生成随机数。 

     二、生成正态分布随机数

    由于正态分布在统计学的重要性和普遍性，实践中经常需要生成特定数学期望和方差的正态分布随机数列，这时当然可以使用上述定理来实现，但由于正态分布函数其定义是一个积分形式，求反函数难度较大，只能通过数值计算得出一个近似正态分布函数，其效果不会很理想。幸运的是，我们可以利用中心极限定理去生成正态分布随机数。